Tous les triangles sont isocèles
Dans un vieux manuscrit, on a trouvé le théorème suivant accompagné de sa démonstration et d’un dessin.
"Théorème: tous les triangles sont isocèles. Démonstration:
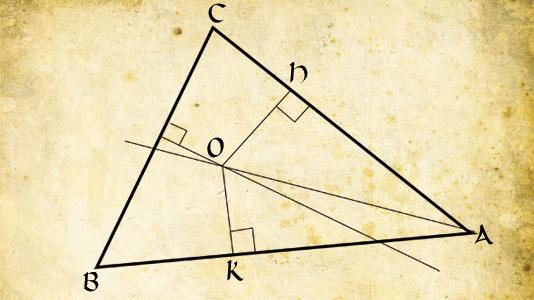
Dans un triangle on trace la bissectrice de l’angle en A et la médiatrice du côté [BC] opposé à A.
Ces deux droites se coupent en O. Notons H et K les pieds des perpendiculaires à [AC] et à [AB] passant par O.
Comme AO est la bissectrice de l’angle en A, les triangles AHO et AKO sont égaux, on peut donc en déduire que AH =AK et HO = KO.
Comme de plus O est sur la médiatrice de [CB] on a l’égalité CO = BO. Ce qui permet par Pythagore de déduire que HC = KB.
Ainsi on a AC = AH + HC = AK + KB = AB.
Le triangle est donc isocèle et donc équilatéral en faisant la même preuve en partant du sommet B."
Puisque tous les triangles ne sont évidemment pas isocèles, il y a une erreur dans cette démonstration. A vous de trouver laquelle!
Vous séchez? La solution!
Publié