Une très grande piscine

L'énigme

Par une journée caniculaire du mois de juin, une bande d’amis se retrouve au bord de la piscine de l’un d’entre eux. Celui-ci rêvait d’une grande piscine ronde et a donc utilisé la surface maximale disponible dans son jardin carré, laissant juste la place pour un petit chemin de 2 mètres sur 9 mètres.

Quelle est la surface totale du jardin ?

La solution

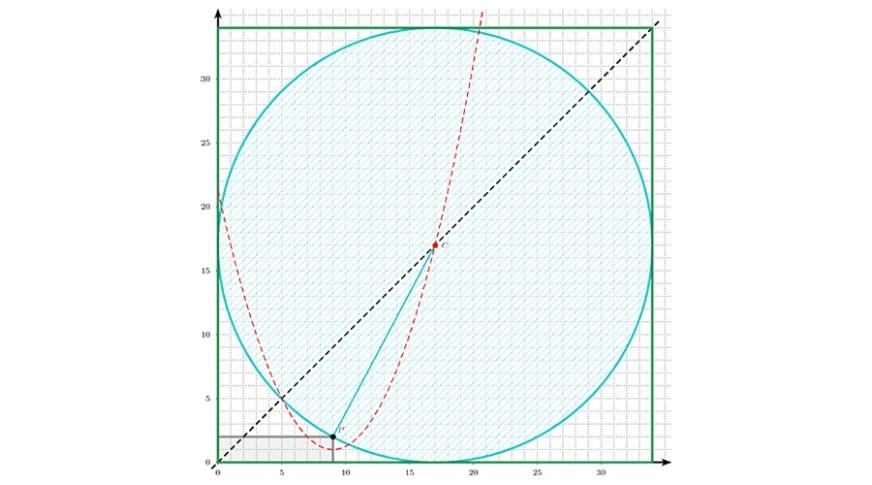
© Mathscope
Croquis du jardin avec le centre de la piscine

Le jardin mesure 34² = 1156 m².

On peut commencer par poser une équation.

Comme le jardin est carré, par symétrie, le centre du cercle doit se situer sur une diagonale du carré. Si on suppose que l’origine d’un système de coordonnées se situe dans l’angle inférieur gauche, le centre du cercle aura pour coordonnées ( coordonnées (a,a). De plus, ce même a sera exactement la longueur du rayon du cercle. L’équation du cercle décrivant la piscine serait donc de la forme :

(x – a)² + (y – b)² = a2

Par ailleurs, le cercle passe par l’extrémité du chemin qui aurait pour coordonnées (9,2). On a ainsi l’équation

(9 – a)² + (2 – b)² = a2

Qu’il suffit de résoudre en a, obtenant ainsi a = 5 ou a = 17. Seule la solution a = 17 satisfait le problème. Le côté du carré vaudra donc 2 × 17 = 34 m et sa surface 34² = 1156 m².

Si on essaye de résoudre graphiquement ce problème à l’aide d’un logiciel de géométrie dynamique, il suffit de se souvenir que la parabole est le lieu des centres des cercles tangents à une droite (la directrice de la parabole) et passant par un point (le foyer de la parabole). En effet, le cercle doit passer par le point P = (9,2) et être tangent au côté inférieur du carré. L’intersection de la parabole (en rouge sur le croquis) avec la diagonale donnera les deux centres possibles dont seul celui de coordonnées (17,17) satisfait la tangence avec tous les côtés du carré.

Mathscope, Université de Genève, RTS Découverte