La solution!

L'énigme

Quatre verres à cocktail sont posés sur une planche horizontale. Cette planche est placée sur trois "cylindres" dont les sections sont illustrées sur le dessin. Le rose est à section circulaire (c'est donc un vrai cylindre) tandis que les sections des deux autres sont des figures constituées d'arcs de cercle.

Pour l'instant, tout est en équilibre; mais que va-t-il se passer si les trois "cylindres" commencent à tourner? La planche restera-t-elle horizontale ou les trois verres vont tomber?

La solution

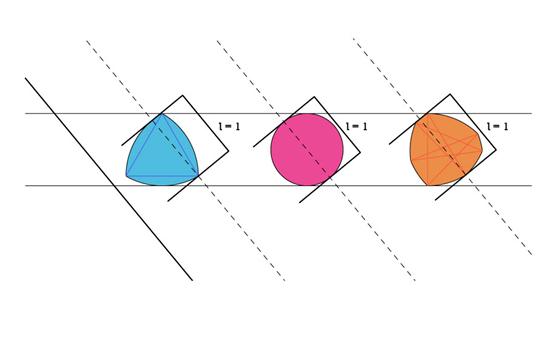
Lorsque les "cylindres" vont se mettre à tourner, la planche restera horizontale et les cocktails ne se renverseront pas.

En effet, les trois sections des "cylindres" sont des figures à diamètre constant.

Autrement dit, si vous prenez un pied à coulisse, quelle que soit la direction dans laquelle vous mesurez le diamètre de l’objet, vous aurez toujours la même valeur.

Cette propriété et très claire pour le cercle (la figure rose). Mais il existe d’autres figures ayant cette propriété dont, par exemple, les deux autres figures proposées.

Celle de gauche est un Triangle de Reuleaux, du nom de l’ingénieur allemand Franz Reuleaux qui est le premier à avoir étudié ses applications en mécanique. Cette figure était bien connue depuis  le Moyen-âge, puisqu’on la retrouve sur des façades d’églises ou dans un manuscrit de Léonard de Vinci.

Si vous voulez en savoir plus sur les figures à diamètre constant, venez nous rendre visite du 7 au 10 octobre sur la plaine de Plainpalais, stand de l’UNIGE à l’occasion de la tournée nationale "Recherche Live" de l’Académie suisse des sciences naturelles (SCNAT). Plus d’infos sur: http://www.sciencesnaturelles.ch/research_live et www.unige.ch/-/recherchelive.