![Les chevaliers de la table ronde [© Erica Guilane Nachez]](https://img.rts.ch/articles/2015/image/34862n-27764541.image?w=1280&h=720 "Les chevaliers de la table ronde [© Erica Guilane Nachez]")
La solution!
Tous les mois, retrouvez ici le problème de maths du mois concocté pour vous par le Mathscope de l'Université de Genève, avec, quelque temps plus tard, sa solution. En ce mois de novembre, on vous demande de dresser la table du roi Arthur et de ses chevaliers de façon équitable.
L'énigme
Le roi Arthur et neuf chevaliers sont assis autour de la table ronde. Le roi a 10 assiettes devant lui; les chevaliers n'ont aucune assiette. En une étape, une personne ayant au moins deux assiettes est autorisée à donner une de ses assiettes à son voisin à gauche et, en même temps, une autre de ses assiettes à son voisin à droite. Peut-on obtenir une situation telle que chaque personne ait exactement une assiette?
La solution
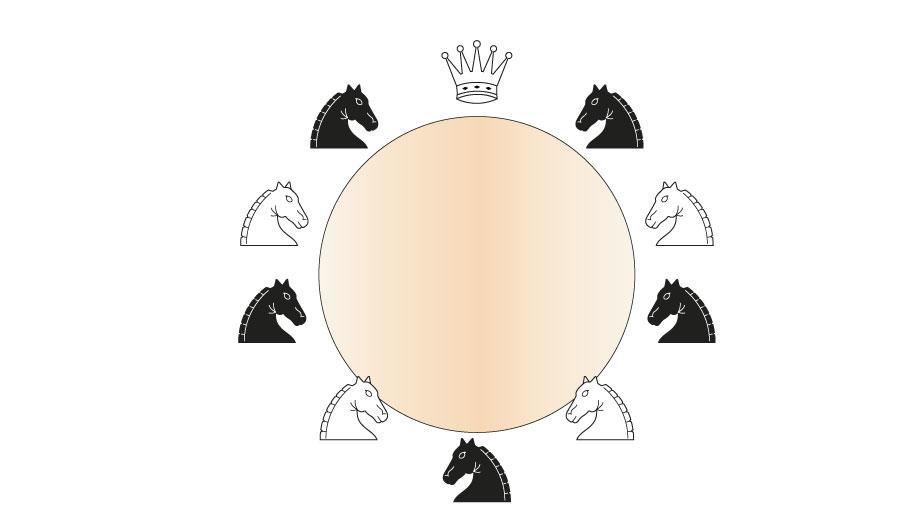
Il n'est pas possible de distribuer les assiettes de façon à ce que chaque chevalier en ait une devant soi. En effet, séparons les chevaliers en deux groupes comme sur le dessin. On remarque que chaque fois qu'un chevalier du groupe blanc distribue deux assiettes, ces deux assiettes arrivent dans les mains d'un chevalier du groupe noir. Autrement dit, lors de chaque mouvement, on ne peut transférer qu'un nombre pair d’assiettes.
Or, chaque groupe est formé de 5 chevaliers. Comme au départ le roi Arthur possède 10 assiettes (un nombre pair d'assiettes), et que 5 n'est pas pair, on ne pourra jamais distribuer les assiettes de façon à ce que chaque chevalier en ait une devant soi.
Mathscope, Université de Genève, RTSdécouverte
Publié